Lý thuyết Toán 6 Bài 10: Số nguyên tố, hợp số và cách phân tích một số ra thừa số nguyên tố?

1. Số nguyên tố là gì? hợp số là gì?

• Số nguyên tố là gì?

- Số nguyên tố là số tự nhiên lớn hơn 1 và chi có hai ước là 1 và chính nó.

* Ví dụ 1: Ư(13) ={1; 13} nên 13 là số nguyên tố.

Các số nguyên tố đầu tiên là: 2, 3, 5, 7, 11, 13, ..

• Hợp số là gì?

- Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn 2 ước.

* Ví dụ 2: Số 12 có 6 ước là 1; 2; 3; 4; 6; 12 nên 12 là hợp số

* Ví dụ 3: a) Trong các số 11; 12; 25, số nào là số nguyên tố, số nào là hợp số? Vì sao?

b) Lan nói rằng: "Nếu một số tự nhiên không là số nguyên tố thì nó phải là hợp số". Em có đồng ý với Lan không? Vì sao?

> Lời giải:

a) Ta có:

 Ư(11) = {1; 11};

 Ư(12) = {1; 2; 3; 4; 6; 12};

 Ư(25) = {1; 5; 25}

⇒ Số 11 là số nguyên tố vì 11 chỉ có hai ước là 1 và chính nó. Số 12 và 25 là hợp số vì chúng có nhiều hơn 2 ước.

b) Em không đồng ý với Lan vì số 0 và số 1 không là số nguyên tố cũng không là hợp số.

2. Phân tích một số ra thừa số nguyên tố

a) Thế nào là phân tích một số ra thừa số nguyên tố

- Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

* Ví dụ: - Số 17 là số nguyên tố và dạng phân tích ra thừa số nguyên tố của nó là 17.

- Số 18 là hợp số và 18 được phân tích ra thừa số nguyên tố là: 18 = 2.3.3 (hoặc viết gọn là 18 = 2.3²)

> Lưu ý:

- Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích các thừa số nguyên tố.

- Mỗi số nguyên tố chỉ có một dạng phân tích ra thừa số nguyên tố là chính số đó.

- Có thể viết gọn dạng phân tích một số ra thừa số nguyên tố bằng cách dùng lũy thừa.

b) Cách phân tích một số ra thừa số nguyên tố

* Cách 1: Phân tích một số ra thừa số nguyên tố theo cột dọc.

- Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.

* Ví dụ: Để phân tích số 280 ra thừa số nguyên tố theo cột dọc, ta lần lượt chia 280 cho các ước số của nó như sau: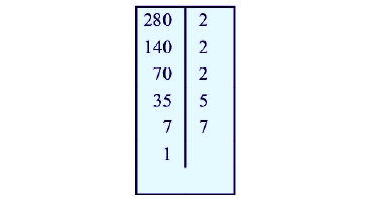

Vậy 280 = 2³ . 5 . 7

> Chú ý: Viết các thừa số nguyên tố theo thứ tự từ bé đến lớn, tích các thừa số giống nhau dưới dạng lũy thừa.

* Cách 2: Phân tích một số ra thừa số nguyên tố theo sơ đồ cây.

- Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.

- Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.

- Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.

- Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.

* Ví dụ: Số 24 được phân tích ra thừa số nguyên tố theo sơ đồ cây như sau:

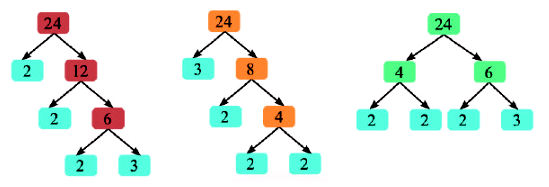
Vậy 24 = 2.2.2.3 = 2³.3

* Nhận xét: Khi phân tích một số ra thừa số nguyên tố theo sơ đồ cây, có thể có nhiều dạng cây khác nhau nhưng kết quả ra thừa số nguyên tố phải giống nhau.