Bảng giá trị và cách vẽ đồ thị của Hàm số bậc nhất y = ax + b? Toán 8 chân trời tập 2 chương 5 bài 3
Trong chương trình Toán 8 Chân trời sáng tạo, bài học về Hàm số bậc nhất là nền tảng quan trọng giúp các em làm quen với đại số sơ cấp.
Khái niệm hàm số bậc nhất là gì, cách lập bảng giá trị và vẽ đồ thị như thế nào? Tất cả sẽ được giải đáp chi tiết trong bài viết này.
1. Hàm số bậc nhất
• Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b với a, b là các số cho trước và a ≠ 0.
* Ví dụ:
Hàm số: y = 4x – 7; y = –6x – 4; y = 4x; s = 5v + 8; m = 30n – 25 là các hàm số bậc nhất .
y = x2; y = 3/x không phải hàm số bậc nhất.
2. Bảng giá trị của hàm số bậc nhất.
• Để lập bảng giá trị của hàm số bậc nhất y = ax + b ta lần lượt cho x nhận các giá trị x1, x2, x3, ... (x1, x2, x3, ... tăng dần) và tính các giá trị tương ứng của y rồi ghi vào bảng có dạng sau:

* Chú ý: Trong bảng giá trị của hàm số bậc nhất y = ax + b, khi giá trị của x tăng dần:
– Nếu a > 0 thì giá trị của y tăng dần
– Nếu a < 0 thì giá trị của y giảm dần
* Ví dụ: Lập bảng giá trị của các hàm số bậc nhất sau:
y = f(x) = 4x – 1
y = g(x) = –0,5x + 8
Với x lần lượt bằng –3; –2; –1; 0; 1; 2; 3. Trong mỗi bảng vừa lập, khi x tăng thì y tăng hay giảm.
* Lời giải:
• Bảng giá trị của hàm số y = f(x) = 4x – 1 như sau:
| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| y = f(x) = 4x – 1 | –13 | –9 | –5 | –1 | 3 | 7 | 11 |
Ta thấy khi x tăng thì y tăng.
• Bảng giá trị của hàm số y = g(x) = –0,5x + 8 như sau:
| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| y = g(x) = –0,5x + 8 | 9,5 | 9 | 8,5 | 8 | 7,5 | 7 | 6,5 |
Ta thấy khi x tăng thì y giảm.
3. Các vẽ đồ thị của hàm số bậc nhất.
3.1. Đồ thị của hàm số y = ax (a ≠ 0)
Để vẽ đồ thị của hàm số y = ax (a ≠ 0), ta thực hiện các bước sau:
+ Bước 1: Xác định một điểm M trên đồ thị khác gốc toạ độ O, chẳng hạn M(1; a)
+ Bước 2: Vẽ đường thẳng qua hai điểm O và M
* Chú ý: Đồ thị của hàm số y = ax còn được gọi là đường thẳng y = ax
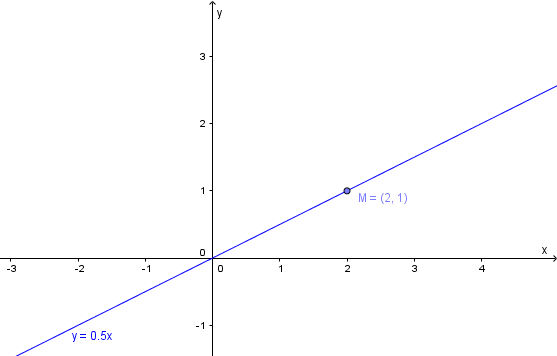
* Ví dụ: Vẽ đồ thị của hàm số y = 0,5x;
* Lời giải:
Cho x = 2 thì y = 0,5.2 = 1 nên điểm M(2; 1)
Ta có đồ thị hàm số của y = 0,5x như sau:
3.2. Đồ thị của hàm số y = ax + b (a ≠ 0, b ≠ 0)
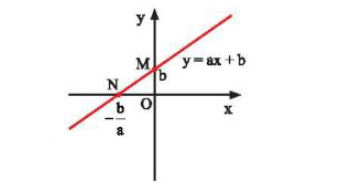
• Đồ thị hàm số y = ax + b (a ≠ 0, b ≠ 0) là một đường thẳng
– Cắt trục tung tại điểm có tung độ bằng b;
– Song song với đường thẳng y = ax.
• Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0, b ≠ 0)
Để vẽ đồ thị hàm số y = ax + b, ta chỉ cần xác định được hai điểm phân biệt tuỳ ý thuộc đồ thị rồi vẽ đường thẳng đi qua hai điểm đó.
Thông thường ta xác định hai điểm đặc biệt là giao của đồ thị với 2 trục toạ độ.
+ Bước 1: Cho x = b thì y = b, ta được điểm M(0; b) trên Oy.
Cho y = 0 thì x = –b/a, ta được điểm N(–b/a; 0) trên Ox
+ Bước 2: Vẽ đường thẳng đi qua hai điểm M và N, ta được đồ thị của hàm số y = ax + b.
* Chú ý: Đồ thị của hàm số y = ax + b còn gọi là đường thẳng y = ax + b
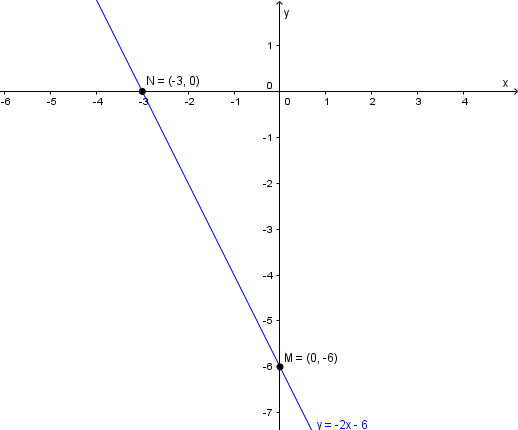
* Ví dụ: Vẽ đồ thị của hàm số y = –2x – 6
* Lời giải:
Cho x = 0 thì y = –6
Cho y = 0 thì x = –3
Đồ thị hàm số y = –2x – 6 là đường thẳng đi qua hai điểm M(0; –6) và điểm N(–3; 0) như sau:
4. Những lưu ý quan trọng
-
Đồ thị hàm số bậc nhất còn được gọi là đường thẳng $y = ax + b$.
-
Hệ số $a$ được gọi là hệ số góc, hệ số $b$ gọi là tung độ gốc.
-
Việc nắm vững cách tìm giao điểm với các trục tọa độ giúp các em vẽ hình nhanh và chính xác nhất trong các bài kiểm tra.
Hy vọng bài viết này giúp các em học sinh lớp 8 nắm vững kiến thức về Bài 3 chương 5 Toán 8 Chân trời sáng tạo. Chúc các em học tốt!
• Xem thêm:
Lý thuyết Toán 8 chân trời tập 2 chương 5 bài 1
Đánh giá & nhận xét
-
 Phân biệt Xác suất lí yhuyết và Xác suất thực nghiệm - Toán 8 chân trời tập 2 chương 9 bài 2
Phân biệt Xác suất lí yhuyết và Xác suất thực nghiệm - Toán 8 chân trời tập 2 chương 9 bài 2
-
 Xác Suất Bằng Tỉ Số: Công Thức và Ví Dụ Minh Họa Dễ Hiểu - Toán 8 chân trời tập 2 chương 9 bài 1
Xác Suất Bằng Tỉ Số: Công Thức và Ví Dụ Minh Họa Dễ Hiểu - Toán 8 chân trời tập 2 chương 9 bài 1
-
 Các trường hợp đồng dạng của tam giác vuông? Toán 8 chân trời tập 2 chương 8 bài 3
Các trường hợp đồng dạng của tam giác vuông? Toán 8 chân trời tập 2 chương 8 bài 3
-
 Các trường hợp (3 trường hợp) đồng dạng của hai tam giác? Toán 8 chân trời tập 2 chương 8 bài 2
Các trường hợp (3 trường hợp) đồng dạng của hai tam giác? Toán 8 chân trời tập 2 chương 8 bài 2
-
 Hai tam giác đồng dạng Khái niệm, Tính chất, Định lí? Toán 8 chân trời tập 2 chương 8 bài 1
Hai tam giác đồng dạng Khái niệm, Tính chất, Định lí? Toán 8 chân trời tập 2 chương 8 bài 1
-
 Tính chất đường phân giác của tam giác và áp dụng? Toán 8 chân trời tập 2 chương 7 bài 3
Tính chất đường phân giác của tam giác và áp dụng? Toán 8 chân trời tập 2 chương 7 bài 3
-
 Khái niệm, tính chất Đường trung bình của tam giác? Toán 8 chân trời tập 2 chương 7 bài 2
Khái niệm, tính chất Đường trung bình của tam giác? Toán 8 chân trời tập 2 chương 7 bài 2
-
 Định lí Thalès, định lí Thalès đảo và hệ quả của định lí Thales trong tam giác? Toán 8 chân trời tập 2 chương 7 bài 1
Định lí Thalès, định lí Thalès đảo và hệ quả của định lí Thales trong tam giác? Toán 8 chân trời tập 2 chương 7 bài 1
-
 Giải bài toán bằng cách lập phương trình bậc nhất? Toán 8 chân trời tập 2 chương 6 bài 2
Giải bài toán bằng cách lập phương trình bậc nhất? Toán 8 chân trời tập 2 chương 6 bài 2
-
 Phương trình bậc nhất một ẩn và cách giải? Toán 8 chân trời tập 2 chương 6 bài 1
Phương trình bậc nhất một ẩn và cách giải? Toán 8 chân trời tập 2 chương 6 bài 1
-
 Hệ số góc của đường thẳng, điều kiện hai đường thẳng song song, cắt nhau? Toán 8 chân trời tập 2 chương 5 bài 4
Hệ số góc của đường thẳng, điều kiện hai đường thẳng song song, cắt nhau? Toán 8 chân trời tập 2 chương 5 bài 4
-
 Toạ độ 1 điểm trên mặt phẳng toạ độ và đồ thị của hàm số? Toán 8 chân trời tập 2 chương 5 bài 2
Toạ độ 1 điểm trên mặt phẳng toạ độ và đồ thị của hàm số? Toán 8 chân trời tập 2 chương 5 bài 2
-
 Khái niệm hàm số là gì, giá trị của hàm số tại 1 điểm? Toán 8 chân trời tập 2 chương 5 bài 1
Khái niệm hàm số là gì, giá trị của hàm số tại 1 điểm? Toán 8 chân trời tập 2 chương 5 bài 1
-
 Mục lục SGK Toán 8 tập 2 Chân trời sáng tạo - Lý thuyết và bài tập Toán 8 tập 2 Chân trời sáng tạo
Mục lục SGK Toán 8 tập 2 Chân trời sáng tạo - Lý thuyết và bài tập Toán 8 tập 2 Chân trời sáng tạo


















































