Bài 9.9 SGK Toán 8 tập 2 Kết nối tri thức

Bài 9.9 SGK Toán 8 Tập 2 Kết nối tri thức:

Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho ∠ABN = ∠ACM

a) Chứng minh rằng ΔABN ∽ ΔACM.

b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB . IN = IC . IM.

Giải bài 9.9 SGK Toán 8 Tập 2 Kết nối tri thức:

Ta có hình vẽ minh hoạ sau:

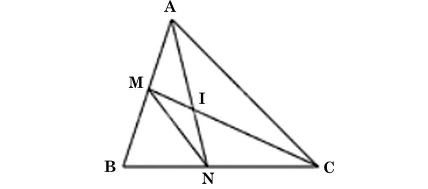
a) Xét tam giác ABN và tam giác ACM:

Góc A chung

 (giả thiết)

⇒ ΔABN ∽ ΔACM (g.g)

b) Vì ΔABN ∽ ΔACM (chứng minh trên) nên

Lại có:

 (hai góc kề bù)

 (hai góc kề bù)

Nên suy ra: 

Xét tam giác IBM và tam giác ICN có:

 (chứng mình trên)

 (vì )

⇒ ΔIBM ∽ ΔICN (g.g).

⇒ IB . IN = IC . IM (đpcm).