Giải bài 3.24 trang 63 Toán 8 Tập 1 SGK Kết nối tri thức

Đề bài:

Cho ba điểm không thẳng hàng.

a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành. Hãy vẽ hình và mô tả cách tìm.

b) Hỏi tìm được bao nhiêu điểm như vậy?

Phân Tích và Hướng Dẫn Giải:

Để giải quyết bài toán này, các em cần nhớ lại dấu hiệu nhận biết hình bình hành: một tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

a) Tìm một điểm để tạo thành hình bình hành:

• Gọi ba điểm đã cho là A, B, C.

• Ta cần tìm điểm D sao cho ABCD là hình bình hành.

• Nếu ABCD là hình bình hành, hai đường chéo AC và BD sẽ cắt nhau tại trung điểm của mỗi đường.

• Do đó, trung điểm của AC phải trùng với trung điểm của BD.

b) Tìm số lượng điểm D:

• Ba điểm không thẳng hàng A, B, C có thể tạo thành ba cặp đường chéo khác nhau: (A, C), (B, C), (A, B).

• Mỗi cặp đường chéo này sẽ tạo ra một trung điểm, từ đó suy ra một vị trí duy nhất cho điểm D.

Lời giải chi tiết:

a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành.

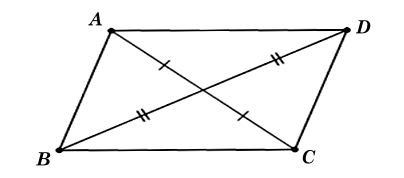
- Gọi ba điểm không thẳng hàng đó là A, B, C. Khi đó ta cần tìm điểm D để bốn điểm A, B, C, D là bốn đỉnh của một hình bình hành (H).

- Nếu đỉnh đối của D trong hình bình hành (H) là B thì trung điểm của BD trùng với trung điểm của AC;

- Ngược lại, lấy điểm D sao cho trung điểm của BD trùng với trung điểm của AC thì (H) là hình bình hành ABCD cần tìm.

b) Tìm được bao nhiêu điểm như vậy?

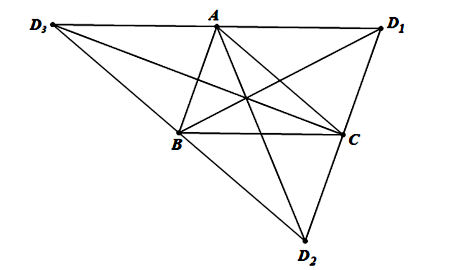
Từ câu a, suy ra có ba điểm D như vậy là D₁, D₂ và D₃.

• Khi D là đỉnh đối của B thì theo câu a, (H) là hình bình hành ABCD₁;

• Khi D là đỉnh đối của A thì (H) là hình bình hành ABD₂C;

• Khi D là đỉnh đối của C thì (H) là hình bình hành ACBD₃.