Giải bài 3.23 trang 63 Toán 8 Tập 1 SGK Kết nối tri thức

Bài 3.23 trang 63 Toán 8 Tập 1 Kết nối tri thức:

Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:

a) Hai tứ giác AEFD, ABFC là những hình bình hành;

b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.

Giải bài 3.23 trang 63 Toán 8 Tập 1 Kết nối tri thức:

Ta có hình minh hoạ như sau:

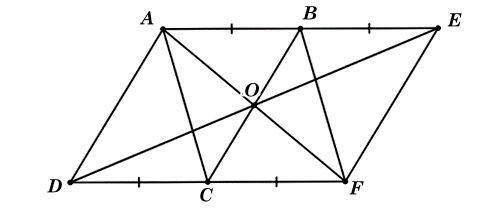
a) Hai tứ giác AEFD, ABFC là những hình bình hành

Vì ABCD là hình bình hành nên AB = CD; AB // CD.

Mà hai điểm B, C lần lượt là trung điểm AE, DF.

⇒ AE = DF; AB = BE = CD = CF.

Tứ giác AEFD có AE // DF (vì AB // CD); AE = DF (chứng minh trên).

⇒ Tứ giác AEFD là hình bình hành.

Tứ giác ABFC có AB // CF (vì AB // CD); AB = CF (chứng minh trên).

⇒ Tứ giác ABFC là hình bình hành.

Như vậy, hai tứ giác AEFD, ABFC là những hình bình hành.

b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.

Vì hình bình hành AEFD có hai đường chéo AF và DE nên chúng cắt nhau tại trung điểm của mỗi đường, ta gọi giao điểm đó là O.

Hình bình hành AEFC có hai đường chéo AF và BC.

Mà O là trung điểm của AF.

⇒ O cũng là trung điểm của BC.

Vậy các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.