Căn bậc hai số học là gì, Khái niệm Số vô tỉ, Cách tính căn bậc hai bằng máy tính? Toán 7 chân trời Tập 1 chương 2 Bài 1

Khái niệm căn bậc hai số học là gì, Số vô tỉ là gì, Cách tính căn bậc hai bằng máy tính cần tay như thế nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Biểu diễn thập phân của một số hữu tỉ

Với một số hữu tỉ , ta chỉ có hai trường hợp sau:

• Trường hợp 1: Nếu  bằng một phân số thập phân thì kết quả của phép chia  là số thập phân bằng với phân số thập phân đó.

* Ví dụ: 

Khi đó, các số 0,6 và 0,08 được gọi là số thập phân hữu hạn.

• Trường hợp 2: Nếu  không bằng bất cứ phân số thập phân nào thì kết quả của phép chia  không bao giờ dừng và có chữ số hoặc cụm chữ số sau dấu phẩy lặp đi lặp lại.

* Ví dụ: 

a) Ta thực hiện phép chia 5 : 12 = 0,41666…; số 6 được lặp đi lặp lại mãi mãi.

Khi đó, ta viết: 

b) Ta thực hiện phép chia 7 : 30 = 0,2333… ; chữ số 3 lặp đi lặp lại mãi mãi.

Khi đó, ta viết: 

Do đó các số 0,41(6); 0,2(3) gọi là các số thập phân vô hạn tuần hoàn và chữ số lặp đi lặp lại như (6); (3) được gọi là chu kì.

* Chú ý: Số 0,41(6) đọc là 0,41 chu kì 6 ; số 0,2(3) đọc là 0,2 chu kì 3.

• Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn.

* Ví dụ: 

2. Số vô tỉ

– Số thập phân vô hạn mà ở phần thập phân của nó không có một chu kì nào cả được gọi là số thập phân vô hạn không tuần hoàn.

– Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ.

– Tập hợp các số vô tỉ kí hiệu là I.

* Ví dụ:

a) Với x² = 2 người ta tính được x = 1,414213562… là số thập phân vô hạn không tuần hoàn.

Vậy x = 1,414213562… là số vô tỉ.

b) Số Pi (π) là tỉ số giữa chu vi của một đường tròn với độ dài đường kính của đường tròn đó.

Người ta tính được π = 3,14159265358979323846264338… là số thập phân vô hạn không tuần hoàn.

Vậy π là một số vô tỉ.

3. Căn bậc hai số học

– Căn bậc hai số học của một số a không âm là số x không âm sao cho x² = a.

– Căn bậc hai số học của số a được kí hiệu là  

– Một số không âm có đúng một căn bậc hai số học.

* Chú ý:

– Số âm không có căn bậc hai số học.

– Ta có  ≥ 0 với mọi số a không âm

– Với mọi số a không âm, ta luôn có 

* Ví dụ: 

– Ta có  là độ dài đường chéo của một hình vuông có cạnh bằng 1.

* Ví dụ: 

4. Tính căn bậc hai số học bằng máy tính cầm tay

Ta có thể tính giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số nguyên dương bằng máy tính cầm tay.

* Ví dụ: Dùng máy tính cầm tay ta tính   và  như sau:

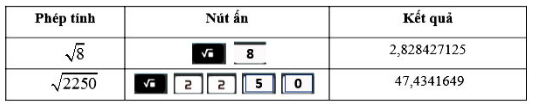
Vậy  ≈ 2,828427125;  ≈ 47,4341649.