Hotline 0939 629 809

Bài 9.7 trang 90 Toán 8 Tập 2 Kết nối tri thức

14:42:3115/01/2024

Hướng dẫn giải bài 9.7 trang 90 Toán 8 tập 2 Kết nối tri thức nội dung SGK chi tiết dễ hiểu nhất giúp học sinh vận dụng giải Toán 8 kết nối tri thức tập 2 tốt hơn, dễ dàng hơn.

Bài 9.7 trang 90 Toán 8 Tập 2 Kết nối tri thức:

Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng ΔA′B′C′ ∽ ΔABC.

Chứng minh rằng: $\frac{A'M'}{AM}=\frac{B'N'}{BN}=\frac{C'P'}{CP}$

Giải Bài 9.7 trang 90 Toán 8 Tập 2 Kết nối tri thức:

Ta có hình minh hoạ sau:

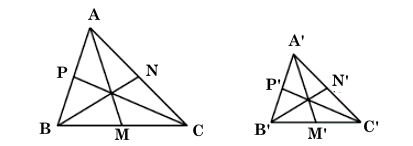
Giải Bài 9.7 trang 90 Toán 8 Tập 2 Kết nối tri thức

Vì ΔA′B′C′ ∽ ΔABC nên: $\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}$ (1) $\frac{A' B'}{A B} = \frac{B' C'}{B C} = \frac{A' C'}{A C}$

Và $\widehat{ABC}=\widehat{A'B'C'}$ ; $\widehat{BCA}=\widehat{B'C'A'}$ ; $\widehat{CAB}=\widehat{C'A'B'}$ (2)

Xét tam giác A'B'M' và ABM có:

$\frac{B'M'}{BM}=\frac{\frac{B'C'}{2}}{\frac{BC}{2}}=\frac{B'C'}{BC}=\frac{B'A'}{BA}$ (theo (1))

$\widehat{A'B'M'}=\widehat{A'B'C'}=\widehat{ABC}=\widehat{ABM}$ (theo (2))

Nên ΔA′M′B′ ∽ ΔAMB (c.g.c)

$\Rightarrow \frac{A'M'}{AM}=\frac{A'B'}{AB}$ (3)

Tương tự, có ΔA′C′P′ ∽ ΔACP

$\Rightarrow \frac{C'P'}{CP}=\frac{A'C'}{AC}$ (4)

Và ΔA′B′N′ ∽ ΔABN

$\Rightarrow \frac{B'N'}{BN}=\frac{A'B'}{AB}$ (5)

Từ (1), (3), (4) và (5) ta có:

$\frac{A'M'}{AM}=\frac{B'N'}{BN}=\frac{C'P'}{CP}$

Với nội dung bài 9.7 trang 90 Toán 8 tập 2 Kết nối tri thức và cách giải chi tiết, dễ hiểu ở trên, Hay Học Hỏi hy vọng giúp các em nắm vững phương pháp giải Toán 8 Kết nối tri thức tập 2. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để được ghi nhận và hỗ trợ, chúc các em học tốt.

• Xem thêm giải Toán 8 Kết nối tri thức tập 2

> Bài 9.5 trang 90 Toán 8 Tập 2 Kết nối tri thức: Giả thiết nào dưới đây chứng tỏ rằng hai tam giác đồng dạng? a) Ba cạnh của tam giác này tỉ lệ với ba cạnh...

> Bài 9.6 trang 90 Toán 8 Tập 2 Kết nối tri thức: Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4 cm, 8 cm và 10 cm. Tam giác...

> Bài 9.7 trang 90 Toán 8 Tập 2 Kết nối tri thức: Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến...

> Bài 9.8 trang 90 Toán 8 Tập 2 Kết nối tri thức: Cho tam giác ABC có AB = 12 cm, AC = 15 cm. Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho AM...

> Bài 9.9 trang 90 Toán 8 Tập 2 Kết nối tri thức: Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho ∠ABN = ∠ACM...

> Bài 9.10 trang 90 Toán 8 Tập 2 Kết nối tri thức: Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3 m và 2 m. Người ta nối...