Phép tính Logarit là gì, tính chất của logarit, công thức đổi cơ số? Toán 11 chân trời tập 2 chương 6 bài 2

Khái niệm Căn bậc n là gì, tính chất của căn bậc n và tính chất của lũy thừa với số mũ thực như nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Khái niệm logarit

• Cho hai số thực dương a, b với a ≠ 1. Số thực α thỏa mãn đẳng thức a^α = b được gọi là logarit cơ số a của b và kí hiêu là log_ab.

α = log_ab ⇔ a^α = b

* Ví dụ: Viết các đẳng thức lũy thừa sau thành đẳng thức logarit

a) 2⁵ = 32

b) 5^–2 = 1/25

* Lời giải:

a) 2⁵ = 32 ⇒ log₂32 = 5

b) 5^–2 = 1/25 ⇒ log₅(1/25) = –2

* Chú ý:

i) Biểu thức log_ab chỉ có nghĩa khi a > 0, a ≠ 1 và b > 0

ii)  Từ định nghĩa logarit, ta có:

log_a1 = 0;   (1)

log_aa = 1;   (2)

log_aa^b = b;  (3)

b^log_ab = b;   (4)

Hai công thức (3) và (4) cho thấy phép lấy logarit và phép nâng lên lũy thừa là hai phép toán ngược nhau.

2. Tính logarit bằng máy tính cầm tay

Sử dụng máy tính cầm tay ta có thể tính nhanh giá trị của các logarit (thường cần lấy giá trị gần đúng bằng cách làm tròn đến hàng nào đó).

* Chú ý:

i) Lôgarit cơ số 10 được gọi là lôgarit thập phân. Ta viết logN hoặc lgN thay cho log₁₀N

ii) Lôgarit cơ số e còn được gọi là logarit tự nhiên. Ta viết lnN thay cho log_eN

* Ví dụ: Sử dụng máy tính cầm tay, tính giá trị của các biểu thức sau (làm tròn đến chữ số thập phân thứ 6).

a) log₃5

b) log0,2

c) ln10

* Lời giải:

3. Tính chất của phép tính logarit

Phép tính logarit có các tính chất sau:

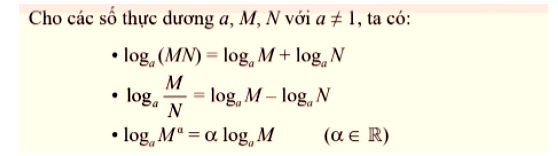
* Chú ý: Đặt biệt, với a, M, N dương a ≠ 1, ta có:

 (với n ∈ N^*)

4. Công thức đổi cơ số

Ta có công thức đổi cơ số như sau:

Đặc biệt, ta có:

* Ví dụ: Tính giá trị của các biểu thức logarit sau:

a) 

b) log₄5.log₅6.log₆8

* Lời giải:

a)

b)