Phương trình, bất phương trình mũ và logarit? Toán 11 chân trời tập 2 chương 6 bài 4

Khái niệm phương trình mũ, phương trình logarit, bất phương trình mũ và logarit là gì? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Phương trình mũ

• Phương trình dạng a^x = b, trong đó a và b là những số cho trước, a > 0, a ≠ 1, được gọi là phương trình mũ cơ bản.

• Nghiệm của phương trình mũ cơ bản

Cho phương trình a^x = b (a > 0, a ≠ 1)

Nếu b > 0 thì phương trình luôn có nghiệm duy nhất x = log_ab

Nếu b < 0 thì phương trình vô nghiệm.

* Chú ý:

i) Nếu b = a^α thì ta có a^x = a^α ⇔ x = α

ii) Tổng quát hơn, a^u(x) = a^v(x) ⇔ u(x) = v(x)

2. Phương trình logarit

• Phương trình dạng log_ax = b,  trong đó a và b là những số cho trước, a > 0, a ≠ 1, được gọi là phương trình logarit cơ bản.

• Nghiệm của phương trình logarit cơ bản

Cho phương trình log_ax = b (a > 0, a ≠ 1) luôn có nghiệm duy nhất x = a^b.

* Chú ý: Tổng quát, xét phương trình dạng

log_au(x) = log_av(x) (a > 0, a ≠ 1)     (1)

Giải phương trình (1), trước hết cần đặt điều kiện có nghĩa: u(x) > 0 và v(x) > 0.

Khi đó, (1) được biến đổi thành:

u(x) = v(x)     (2)

Sau khi giải phương trình (2), ta cần kiểm tra sự thoả mã của điều kiện. Nghiệm của phương trình (1) là những nghiệm của (2) thoả mãn điều kiện.

3. Bất phương trình mũ

• Bất phương trình mũ cơ bản là bất phương trình có dạng a^x > b (hoặc a^x ≥ b, a^x < b, a^x ≤ b), với a, b là những số cho trước, a > 0, a ≠ 1.

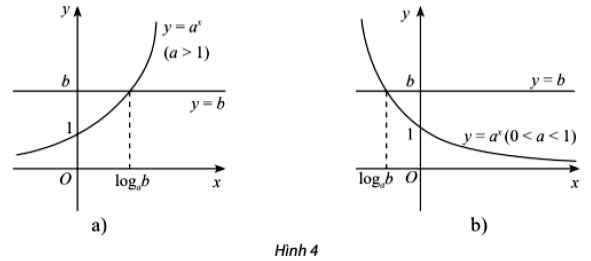
* Chú ý:

i) Tương tự như trên, từ đồ thị hình 4, ta nhận được kết quả về nghiệm của mỗi bất phương trình a^x ≥ b, a^x < b, a^x ≤ b (các bất phương trình a^x < b, a^x ≤ b vô nghiệm nếu b ≤ 0)

ii) Nếu a > 0 thì a^u(x) > a^v(x) ⇔ u(x) > v(x)

Nếu 0 < a < 1 thì a^u(x) > a^v(x) ⇔ u(x) < v(x)

4. Bất phương trình logarit

• Bất phương trình logarit cơ bản là bất phương trình có dạng log_ax > b (hoặc log_ax ≥ b, log_ax < b, log_ax ≤ b), với a, b là những số cho trước, a > 0, a ≠ 1.

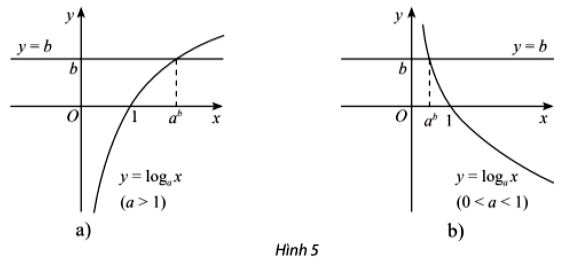
* Chú ý:

i) Tương tự như trên, từ đồ thị hình 5, ta nhận được kết quả về nghiệm của mỗi bất phương trình log_ax ≥ b, log_ax < b, log_ax ≤ b.

ii) Nếu a > 0 thì log_au(x) > log_av(x) ⇔ u(x) > v(x) > 0

Nếu 0 < a < 1 thì log_au(x) > log_av(x) ⇔ 0< u(x) < v(x)