Đạo hàm là gì, số e là gì, cách tính đạo hàm bằng định nghĩa? Toán 11 tập 2 chân trời chương 7 bài 1

Đạo hàm là gì, số e là gì, cách tính đạo hàm bằng định nghĩa như nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Đạo hàm

• Cho hàm số y = f(x) xác định trên khoảng (a; b) và x₀ ∈ (a; b).

Nếu tồn tại giới hạn hữu hạn: 

thì giới hạn này được gọi là đạo hàm của hàm số f(x) tại x₀ , kí hiệu là f'(x) hoặc y'(x₀). Vây:

* Chú ý: Cho hàm số y = f(x) xác định trên khoảng (a; b). Nếu  hàm số này có đạo hàm tại mọi điểm x ∈ (a; b) thì ta nói nó có đạo hàm trên khoảng (a; b), kí hiệu y' hoặc f'(x). 

* Ví dụ: Cho hàm só f(x) = x². Tính f'(x₀) với x₀ ∈ R.

* Lời giải:

Ta có: 

* Chú ý: Cho hàm số y = f(x) xác định trên khoảng (a; b), có đạo hàm tại x₀ ∈ (a; b).

i) Đại lượng Δx = x – x₀ được gọi là số gia của biến tại x₀. Đại lượng Δy = f(x) – f(x₀) gọi là số gia tương ứng của hàm số. Khi đó, x = x₀ + Δx và

ii) Tỉ số Δy/Δx biểu thị tốc độ thay đổi trung bình của đại lượng y theo đại lượng x trong khoảng từ  x₀ đến x₀ + Δx; còn f'(x) biểu thị tốc độ thay đổi (tức thời) của đại lượng y theo đại lượng x tại điểm x₀.

• Ý nghĩa vật lí của đạo hàm

— Nếu hàm số s = f(t) biểu thị quãng đường di chuyển của vật theo thời gian t thì f'(t₀) biểu thị tốc độ tức thời của chuyển động tại thời điểm t₀.

— Nếu hàm số T = f(t) biểu thị nhiệt độ T theo thời gian t thì f'(t₀) biểu thị tốc độ thay đổi nhiệt độ theo thời gian tại thời điểm t₀.

2. Ý nghĩa hình học của đạo hàm

Cho hàm số y = f(x) xác định trên khoảng (a; b) và có đạo hạm tại x₀ ∈ (a; b). Gọi (C) là đồ thị của hàm số đó.

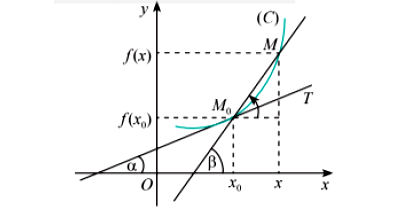
Đạo hàm của hàm số y = f(x) tại điểm x₀ là hệ số góc của tiếp tuyến M₀T của (C) tại điểm M₀(x₀; f(x₀))

Tiếp tuyến M₀T có phương trình là: y – f(x₀) = f'(x₀)(x – x₀)

* Ví dụ: Cho hàm số y = f(x) = x² có đồ thị (C) và điểm M(2; 4) ∈ (C). Tính hệ số góc của tiếp tuyến của (C) tại điểm M và viết phương trình của tiếp tuyến đó.

* Lời giải:

Ta có f'(x) = (x²)' = 2x

Nên tiếp tuyến của (C) tại điểm M(2; 4) có hệ số góc là f'(x_M) = f'(2) = 2.2 = 4

Phương trình tiếp tuyến của (C) tại M có dạng: y – y_M = f'(x_M).(x – x_M)

⇔ y – 4 = 4(x – 2)

⇔ y = 4x – 4

3. Số e là gì

Một người gửi tiết kiệm khoản tiền A triệu đồng (gọi là vốn) với lãi suất là r/năm theo thể thức lãi kép (tiền lãi sau mỗi kì hạn được cộng gộp vào vốn).

* Lưu ý: Nếu 1 năm được chia thành n kì hạn (n ∈ N^*) thì lãi suất mỗi kì hạn là r/n.

Kí hiệu T là tổng số tiền vốn và lãi của người gửi sau một năm. Tuỳ theo kì hạn, ta có công thức tính T khác nhau.

Nếu kì hạn là 1 năm thì T = A(1 + r)

Nếu kì hạn là 6 tháng thì 

Nếu kì hạn là 3 tháng thì

Nếu kì hạn là 1 tháng thì

Nếu kì hạn là 1 ngày thì  (luôn coi 1 năm là 365 ngày)

Tổng quát, nếu 1 năm được chia thành n kì hạn thì:

 với 

Khi kì hạn càng ngắn thì n càng lớn, do đó m càng lớn. Người ta chứng minh được rằng có giới hạn hữu hạn:

Hơn nữa, e là số vô tỉ và e = 2,718281828... (số thập phân vô hạn không tuần hoàn).

Từ kết quả trên suy ra, khi kì hạn trở nên rất ngắn (m dần đến +∞) thì  dần đến e.

Và do đó:  dần đến A.e^r.