Bài 6.19 SGK Toán 10 tập 2 Kết nối tri thức

Bài 6.19 SGK Toán 10 Tập 2 Kết nối tri thức:

Xét đường tròn đường kính AB = 4 và một điểm M di chuyển trên đoạn AB, đặt AM = x (H.6.19). Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ. 

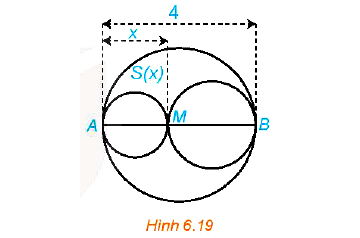
Giải bài 6.19 SGK Toán 10 Tập 2 Kết nối tri thức:

Vì AM = x nên x > 0, lại có AM < AB nên x < 4, vậy điều kiện của x là 0 < x < 4. 

Đường tròn lớn có đường kính AB = 4 nên bán kính của hình tròn này là R = 2. 

Diện tích hình tròn lớn này là S_R = πR² = π . 2² = 4π.  

Đường tròn nhỏ đường kính AM = x có bán kính là r₁ = x/2

Diện tích hình tròn nhỏ có bán kính r₁ là S₁ = πr₁² 

Ta có: AM + MB = AB ⇒ MB = AB – AM = 4 – x. 

Đường tròn đường kính MB có bán kính là 

Diện tích hình tròn có bán kính r₂ là S₂ = πr₂² 

Tổng diện tích hai hình tròn nhỏ là: S₁₂ = S₁ + S₂

Diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ là: S(x) = S_R – S₁₂

Vì diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ hay diện tích S(x) nhỏ hơn hoặc bằng nửa tổng diện tích hia hình tròn nhỏ hay:

Khi đó: 

⇔ – 2x² + 8x ≤ x² – 4x + 8 

⇔ 3x² – 12x + 8 ≥ 0

Xét tam thức f(x) = 3x² – 12x + 8

có ∆' = (– 6)² – 3 . 8 = 12 > 0

nên f(x) có hai nghiệm  và 

Mặt khác hệ số a = 3 > 0, do đó ta có bảng xét dấu f(x): 

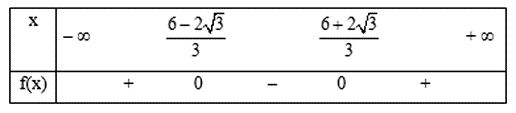
Vì vậy, f(x) ≥ 0 với mọi 

Kết hợp với điều kiện 0 < x < 4. 

Vậy các giá trị của x thỏa mãn yêu cầu của đề bài là: