Hotline 0939 629 809

Tọa độ một điểm, Tọa độ một Vectơ, Tọa độ trung điểm đoạn thẳng và trọng tâm tam giác? Toán 10 chân trời tập 2 chương 9 bài 1

08:03:0926/11/2023

Lý thuyết Bài 1: Tọa độ của Vectơ chương 9 SGK Toán 10 Chân trời sáng tạo Tập 2. Nội dung về trục tọa độ, hệ trục tọa độ, tọa độ của một điểm, tọa độ của một vectơ, tọa độ trung điểm đoạn thẳng và trọng tâm tam giác.

Tọa độ một điểm, Tọa độ một Vectơ, Tọa độ trung điểm đoạn thẳng và trọng tâm tam giác như thế nào? câu trả lời sẽ có ngay trong nội dung bài viết này.

1. Tọa độ của vectơ đối với một hệ trục tọa độ

1.1. Trục tọa độ

Trục tọa độ (gọi tắt là trục) là một đường thẳng trên đó đã xác định một điểm O (gọi là điểm gốc) và một vectơ $\small \overrightarrow{e}$ có độ dài bằng 1 gọi là vectơ đơn vị của trục.

Ta kí hiệu trục đó là (O; $\small \overrightarrow{e}$ ) Trục tọa độ

1.2. Hệ trục tọa độ

• Hệ trục tọa độ (O; $\small \overrightarrow{i}$ ; $\small \overrightarrow{j}$ ) gồm hai trục (O; $\small \overrightarrow{i}$ ) và (O; $\small \overrightarrow{j}$ ) vuông góc với nhau. Điểm gốc O chung của hai trục gọi là gốc tọa độ.

Trục (O; $\small \overrightarrow{i}$ ; $\small \overrightarrow{j}$ ) được gọi là trục hoành và kí hiệu là Ox,

Trục (O; $\small \overrightarrow{j}$ ) được gọi là trục tung và kí hiệu là Oy.

Các vectơ $\small \overrightarrow{i}$ và $\small \overrightarrow{j}$ là các vectơ đơn vị trên Ox và Oy. Hệ trục tọa độ (O; $\small \overrightarrow{i}$ ; $\small \overrightarrow{j}$ ) còn được kí hiệu là Oxy.

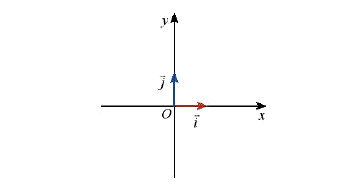
Hệ trục tọa độ

* Chú ý: Mặt phẳng mà trên đó đã cho một hệ trục tọa độ Oxy được gọi là mặt phẳng tọa độ Oxy, hay gọi tắt là mặt phẳng Oxy.

1.3. Tọa độ của một vectơ

Trong mặt phẳng Oxy, cặp số (x; y) trong biểu diễn $\small \overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}$ được gọi là tọa độ của vectơ $\small \overrightarrow{a}$ , kí hiệu $\small \overrightarrow{a}=(x;y)$ , x gọi là hoành độ, y gọi là tung độ của vectơ $\small \overrightarrow{a}$ .

* Ví dụ 1: Trong mặt phẳng Oxy, cho một vectơ $\small \overrightarrow{a}$ tùy ý. Vẽ $\small \overrightarrow{OA}= \overrightarrow{a}$ và gọi A₁, A₂ lần lượt là hình chiếu vuông góc của A lên Ox và Oy (Hình 4). Đặt $\small \overrightarrow{OA}_1= x\overrightarrow{i},\: \overrightarrow{OA}_2= y\overrightarrow{j}$ . Biểu diễn vectơ $\small \overrightarrow{a}$ theo hai vectơ $\small \small \overrightarrow{i}$ và $\small \small \overrightarrow{j}$ .

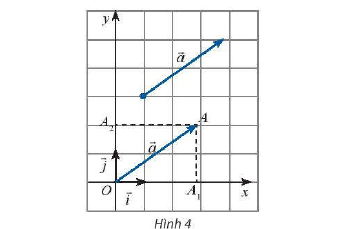Tọa độ của một Vectơ * Lời giải:

Xét bình hành OA₁AA₂, có:

$\small \overrightarrow{OA}=\overrightarrow{OA}_1+\overrightarrow{OA}_2$ (quy tắc hình bình hành)

Suy ra: $\small \overrightarrow{OA}=x\overrightarrow{i}+y\overrightarrow{j}$

Mà $\small \overrightarrow{OA}=\overrightarrow{a}$ nên $\small \overrightarrow{a}=x\overrightarrow{i}+y\overline{j}$

Vậy $\small \overrightarrow{a}=x\overrightarrow{i}+y\overline{j}$

* Ví dụ 2: Cho $\small \overrightarrow{a}=2\overrightarrow{i}+3\overline{j}$

Ta có cặp số (2; 3) là tọa độ của vectơ $\small \overrightarrow{a}$

Ta kí hiệu: $\small \overrightarrow{a}=(2;3)$

Trong đó 2 là hoành độ của vectơ $\small \overrightarrow{a}$ và 3 là tung độ của vectơ $\small \overrightarrow{a}$ .

* Chú ý:

• $\small \overrightarrow{a}=(x;y)\Leftrightarrow \overrightarrow{a}=x\overrightarrow{i}+y\overline{j}$

• Nếu cho $\small \overrightarrow{a}=(x;y)$ và $\small \overrightarrow{b}=(x';y')$ thì $\small \overrightarrow{a}=\overrightarrow{b}\Leftrightarrow \left\{\begin{matrix} x=x'\\ y=y' \end{matrix}\right.$

1.4. Tọa độ của một điểm

Trong mặt phẳng tọa độ, cho một điểm M tùy ý. Tọa độ của vectơ $\small \overrightarrow{OM}$ được gọi là tọa độ của điểm M.

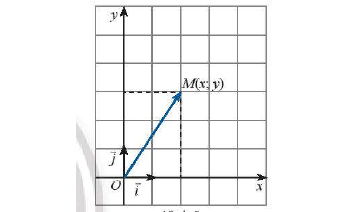
Tọa độ một điểm

* Nhận xét:

• Nếu $\small \overrightarrow{OM}=(x;y)$ thì cặp số (x; y) là tọa độ của điểm M, kí hiệu M(x; y), x gọi là hoành độ, y gọi là tung độ của điểm M.

• M(x; y) ⇔ $\small \overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}$

* Ví dụ: Nếu $\small \overrightarrow{OM}$ = (–5; 2) thì cặp số (–5; 2) là tọa độ của điểm M.

Ta kí hiệu là M(–5; 2).

Trong đó –5 là hoành độ của điểm M và 2 là tung độ của điểm M.

* Chú ý: Hoành độ của điểm M còn được kí hiệu là x_M, tung độ của điểm M còn được kí hiệu là y_M. Khi đó ta viết M(x_M; y_M).

2. Biểu thức tọa độ của các phép toán vectơ

Cho hai vectơ $\small \overrightarrow{a}=(a_1;a_2)$ , $\small \overrightarrow{b}=(b_1;b_2)$ và số thực k. Khi đó:

(1) $\small \overrightarrow{a}+\overrightarrow{b}=(a_1+b_1;a_2+b_2)$

(2) $\small \overrightarrow{a}-\overrightarrow{b}=(a_1-b_1;a_2-b_2)$

(3) $\small k\overrightarrow{a}=(ka_1;ka_2)$

(4) $\small \overrightarrow{a}.\overrightarrow{b}=a_1.b_1+a_2.b_2$

* Ví dụ: Cho hai vectơ $\small \overrightarrow{m}$ = (–6; 1) và $\small \overrightarrow{n}$ = (0; 2).

a) Tìm tọa độ của các vectơ $\small \overrightarrow{m}$ + $\small \overrightarrow{n}$ ; $\small \overrightarrow{m}$ – $\vec{m} - \vec{n}$ ; 10 $\small \overrightarrow{m}$ ; –4 $\small \overrightarrow{n}$

b) Tính các tích vô hướng $\small \overrightarrow{m}$ . $\small \overrightarrow{n}$ ; (10 $\small \overrightarrow{m}$ ).(–4 $\small \overrightarrow{n}$ )

* Lời giải:

a) Ta có:

$\small \overrightarrow{m}$ + $\small \overrightarrow{n}$ = (–6 + 0; 1 + 2) = (–6; 3)

$\small \overrightarrow{m}$ – $\vec{m} - \vec{n}$

$\vec{m} - \vec{n}$

3. Áp dụng của tọa độ vectơ

3.1. Liên hệ giữa tọa độ của điểm và tọa độ của vectơ trong mặt phẳng

Cho hai điểm A(x_A; y_A), B(x_B; y_B).

Ta có: $\small \overrightarrow{AB}=(x_B-x_A;y_B-y_A)$

* Ví dụ: Cho E((9; 9), F(8; -7), G(0; -6). Tìm tọa độ của các vectơ $\small \overrightarrow{FE},\: \overrightarrow{FG},\: \overrightarrow{EG}.$

* Lời giải:

Ta có tọa độ của các vectơ như sau:

$\small \overrightarrow{FE}$ = (9 – 8; 9 – (–7)) = (1; 16);

$\small \overrightarrow{FG}$ = (0 – 8; –6 – (–7)) = (–8; 1);

$\small \overrightarrow{EG}$ = (0 – 9; –6 – 9) = (–9; –15).

3.2. Tọa độ trung điểm của đoạn thẳng và trọng tâm của tam giác

• Cho hai điểm A(x_A; y_A) và B(x_B; y_B). Tọa độ trung điểm M(x_M; y_M) của đoạn thẳng AB là:

$\small x_M=\frac{x_A+x_B}{2}$ , $\small y_M=\frac{y_A+y_B}{2}$

• Cho ∆ABC có A(x_A; y_A), B(x_B; y_B), C(x_C; y_C). Tọa độ trọng tâm G(x_G; y_G) của tam giác ABC là:

$\small x_G=\frac{x_A+x_B+x_C}{3}$ , $\small y_G=\frac{y_A+y_B+y_C}{3}$

* Ví dụ: Cho tam giác QRS có tọa độ các đỉnh là Q(7; -2), R(-4; 9) và S(5; 8).

a) Tìm tọa độ trung điểm M của cạnh QS.

b) Tìm tọa độ trọng tâm G của tam giác QRS.

* Lời giải:

a) Gọi tọa độ của điểm M là M(x_M; y_M). Vì M là trung điểm của QS nên ta có:

$\small x_M=\frac{x_Q+x_S}{2}=\frac{7+5}{2}=6$

$\small y_M=\frac{y_Q+y_S}{2}=\frac{-2+8}{2}=3$

Vậy M(6; 3).

b) Gọi tọa độ của điểm G là G(x_G; y_G). Vì G là trọng tâm của QRS nên ta có:

$\small x_G=\frac{x_Q+x_R+x_S}{3}=\frac{7+(-4)+5}{3}=\frac{8}{3}$

$\small y_G=\frac{y_Q+y_R+y_S}{3}=\frac{(-2)+9+8}{3}=5$

Vậy G(8/3; 5)

3.3. Ứng dụng biểu thức tọa độ của các phép toán vectơ

Cho hai vectơ $\small \overrightarrow{a}=(a_1;a_2)$ , $\small \overrightarrow{b}=(b_1;b_2)$ và hai điểm A(x_A; y_A), B(x_B; y_B). Ta có:

• $\small \overrightarrow{a}\perp \overrightarrow{b}\Leftrightarrow a_1b_1+a_2b_2=0$

• $\small \overrightarrow{a}$ và $\small \overrightarrow{b}$ cùng phương $\small \Leftrightarrow \left\{\begin{matrix} a_1=tb_1\\ a_2=tb_2 \end{matrix}\right.$ hay $\small \left\{\begin{matrix} b_1=ka_1\\ b_2=ka_2 \end{matrix}\right.$ ⇔ a₁b₂ – a₂b₁ = 0;

• $\small \left |\overrightarrow{a} \right |=\sqrt{a_1^2+a_2^2}$

• $\small AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$

• $\small cos(\overrightarrow{a},\overrightarrow{b})=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left |\overrightarrow{a} \right |.\left | \overrightarrow{a} \right |}=\frac{a_1b_+a_2b_2}{\sqrt{a_1^2+a_2^2}.\sqrt{b_1^2+b_2^2}}$ $\small (\overrightarrow{a},\overrightarrow{b}\neq \overrightarrow{0})$

* Ví dụ: Trong mặt phẳng Oxy, cho tam giác DEF có tọa độ đỉnh là D(2; 2), E(6; 2) và F(2; 6).

a) Tìm tọa độ điểm H là chân đường cao của tam giác DEF kẻ từ D.

b) Giải tam giác DEF.

* Lời giải:

a) Gọi H(x_H; y_H).

Ta có: $\small \overrightarrow{DH}=(x_H-2;y_H-2)$ , $\small \overrightarrow{EF}=(-4;4)$ , $\small \overrightarrow{EH}=(x_H-6;y_H-2)$

Vì H thuộc EF nên $\small \overrightarrow{EF}$ và $\small \overrightarrow{EH}$ cùng phương.

$\small \frac{x_H-6}{-4}=\frac{y_H-2}{4}\Leftrightarrow x_H=-y_H+8$

$\small \Rightarrow \overrightarrow{DH}(-y_H+6;y_H-2)$

Vì DH ⊥ EF nên $\small \overrightarrow{DH}.\overrightarrow{FE}=0$

⇔ (–y_H + 6).(–4) + (y_H – 2).4 = 0

⇔ 4y_H – 24 + 4y_H – 8 = 0

⇔ 8y_H = 32

⇔ y_H = 4

⇒ x_H = –4 + 8 = 4

Vậy H(4; 4).

b) Ta có:

$\small \overrightarrow{DE}=(6-2;2-2)=(4;0)$ $\small \Rightarrow DE=\sqrt{4^2+0^2}=4$

$\small \overrightarrow{EF}=(-4;4)\Rightarrow EF=\sqrt{(-4)^2+4^2}=4\sqrt{2}$

$\small \overrightarrow{DF}=(2-2;6-2)=(0;4)$ $\small \Rightarrow DF=\sqrt{0^2+4^2}=4$

Ta lại có: $\small FE^2=(4\sqrt{2})^2=32$

và DE² + DF² = 4² + 4² = 32

Suy ra EF² = DE² + DF²

Theo định lí Py – ta – go đảo ta có: ∆DEF vuông tại D

Mà DE = DF nên tam giác DEF vuông cân tại D.

Suy ra: $\small \widehat{D}=45^0,\widehat{E}=\widehat{F}=45^0$

Vậy DE = DF = 4, EF = 4 $\small \sqrt{2}$ , $\small \widehat{D}=45^0,\widehat{E}=\widehat{F}=45^0$

Với nội dung bài viết về: Tọa độ một điểm, Tọa độ một Vectơ, Tọa độ trung điểm đoạn thẳng và trọng tâm tam giác? Toán 10 chân trời tập 2 chương 9 bài 1 chi tiết, dễ hiểu ở trên. Hay Học Hỏi hy vọng giúp các em nắm vững nội dung Lý thuyết Toán 10 tập 2 SGK Chân trời sáng tạo. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để được ghi nhận và hỗ trợ, chúc các em học tốt.