Lý thuyết Toán 10 bài 2: Tập hợp và các phép toán trên tập hợp (Kết nối tri thức)

1. Các khái niệm cơ bản về tập hợp

1.1. Tập hợp

• Có thể mô tả một tập hợp bằng một trong hai cách sau:

  • Cách 1. Liệt kê các phần tử của tập hợp.

  • Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

• : phần tử a thuộc tập hợp S.

• : phần tử a không thuộc tập hợp S.

Chú ý:

Số phần tử của tập hợp S được kí hiệu là .

Ví dụ:

• Cho tập hợp A là tập hợp các số tự nhiên chia hết cho 2, lớn hơn 5 và nhỏ hơn 15.

  • Ta mô tả tập hợp A bằng hai cách như sau:

    • Cách 1: Liệt kê các phần tử của tập hợp: .

    • Cách 2: Chỉ ra tính chất đặc trưng của các phần tử: .

  • Tập hợp A có 5 phần tử, ta viết: .

  •  thuộc tập hợp A, ta viết  .

  •  không thuộc tập hợp A, ta viết .

• Tập hợp không chứa phần tử nào được gọi là tập rỗng, kí hiệu là .

  Ví dụ:

  • Tập hợp các nghiệm của phương trình  là tập rỗng.

  • Tập hợp những người sống trên Mặt Trời là tập rỗng.

1.2. Tập hợp con

• Nếu mọi phần tử của tập hợp T đều là phần tử của tập hợp S thì ta nói T là một tập hợp con (tập con) của S và viết là  (đọc là T chứa trong S hoặc T là tập con của S).

• Thay cho , ta còn viết  (đọc là S chứa T).

• Kí hiệu  để chỉ T không là tập con của S.

Nhận xét: T là tập con của S nếu mệnh đề sau đúng:  .

Quy ước: Tập rỗng là tập con của mọi tập hợp.

• Minh họa T là một tập con của S bằng biểu đồ Ven.

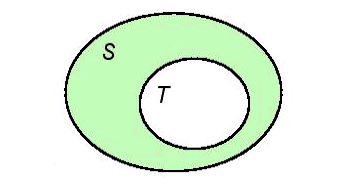
• Ví dụ: Cho các tập hợp:, , .

  • Tập hợp T là tập con của tập hợp S (do mọi phần tử của T đều thuộc S). Ta viết .

  • Tập hợp M không là tập hợp con của tập hợp S (do có phần tử 4 thuộc M nhưng không thuộc S). Ta viết .

1.3. Hai tập hợp bằng nhau

• Hai tập hợp S và T được gọi là hai tập hợp bằng nhau nếu mỗi phần tử của T cũng là phần tử của tập hợp S và ngược lại. Kí hiệu là S = T.

• Nếu và  thì .

  Ví dụ: Cho 2 tập hợp: S = \{n | n là bội chung của 2 và  3; n < 20\}:  và T = {n | n là bội của  6; n < 20}  .

  Ta có: . . Vậy .

2. Các tập hợp số

2.1. Mối quan hệ giữa các tập hợp số

• Tập hợp các số tự nhiên .

• Tập hợp các số nguyên  gồm các số tự nhiên và số nguyên âm: 

  

• Tập hợp các số hữu tỉ  gồm các số được viết dưới dạng phân số , với .

• Tập hợp các số thực  gồm các số hữu tỉ và các số vô tỉ.

• Mối quan hệ giữa các tập hợp số: .

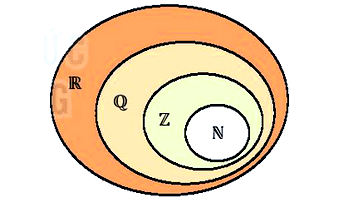
• Ví dụ: Cho tập hợp .

  • Tập hợp B gồm các số nguyên: -1; 2; 4; 10 nên .

  • Các số nguyên cũng là các số hữu tỉ và cũng là các số thực, nên  và .

2.2. Các tập con thường dùng của $\mathbb{R}$

• Một số tập con thường dùng của tập số thực :

  • Khoảng:

    • 

    • 

    • 

    • 

  • Đoạn:

    • 

  • Nửa khoảng:

    • 

    • 

    • 

    •  

Kí hiệu:

• • : Đọc là dương vô cực (hoặc dương vô cùng).

  • : Đọc là âm vô cực (hoặc âm vô cùng).

  • a, b gọi là các đầu mút của đoạn, khoảng hay nửa khoảng.

    Ví dụ:

  • Ta có:  thì ta viết .

  • Ta có: .

3. Các phép toán trên tập hợp

3.1. Giao của hai tập hợp

• Tập hợp gồm các phần tử thuộc cả hai tập hợp S và T gọi là giao của hai tập hợp S và T, kí hiệu là . .

  Ví dụ: Cho 2 tập hợp:  và . Giao của 2 tập hợp trên là tập hợp.

3.2. Hợp của hai tập hợp

• Tập hợp gồm các phần tử thuộc tập hợp S hoặc thuộc tập hợp T gọi là hợp của hai tập hợp S và T, kí hiệu là . .

  Ví dụ: Cho 2 tập hợp:  và .

  Hợp của hai tập hợp trên là .

3.3. Hiệu của hai tập hợp

• Hiệu của hai tập hợp S và T là tập hợp gồm các phần tử thuộc S nhưng không thuộc T,

  kí hiệu là . .

• Nếu  thì được gọi là phần bù của T trong S, kí hiệu là C_S T.

  Ví dụ: Cho các tập hợp: ; ;

  X = {x | x (là các số nguyên dương nhỏ hơn)9}.

• Ta có: . T \setminus . Lại có:\}.

  Vì mọi phần tử của tập S đều thuộc tập X nên .

  Phần bù của S trong X là .