Công thức tích vô hướng của 2 vectơ, biểu thức tọa độ và ứng dụng của tích vô hướng trong không gian - Toán lớp 12

Vậy công thức tích vô hướng của 2 vectơ, biểu thức tọa độ của tích vô hướng trong không gian viết thế nào? ứng dụng của tích vô hướng là gì? chúng ta sẽ cùng tìm hiểu ở bài viết này.

I. Biểu thức tọa độ của các phép toán vectơ

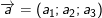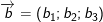• Định lý: Trong không gian Oxyz, cho hai vectơ $\small \overrightarrow{a}=(a_1;a_2;a_3)$ và $\small \overrightarrow{b}=(b_1;b_2;b_3)$ ta có:

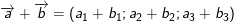
i) $\small \overrightarrow{a}+\overrightarrow{b}=(a_1+b_1;a_2+b_2;a_3+b_3)$

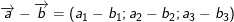
ii) $\small \overrightarrow{a}-\overrightarrow{b}=(a_1-b_1;a_2-b_2;a_3-b_3)$

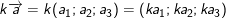iii) $\small k\overrightarrow{a}=k(a_1;a_2;a_3)=(ka_1;ka_2;ka_3)$ với k là số thực.

• Hệ quả:

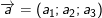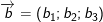
i) Cho hai vectơ $\small \overrightarrow{a}=(a_1;a_2;a_3)$ và $\small \overrightarrow{b}=(b_1;b_2;b_3)$

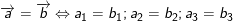
Ta có: $\small \overrightarrow{a} = \overrightarrow{b}\Leftrightarrow a_1=b_1;a_2=b_2;a_3=b_3$

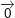ii) Vectơ $\small \overrightarrow{0}$ có tọa độ là (0; 0 ; 0).

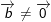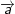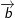iii) Với $\small \overrightarrow{b}\neq \overrightarrow{0}$ thì hai vectơ $\small \overrightarrow{a}$ và $\small \overrightarrow{b}$ cùng phương khi và chỉ khi có một số k sao cho:

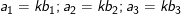
$\small a_1=kb_1;a_2=kb_2;a_3=kb_3$

iv) Trong không gian Oxyz, nếu cho hai điểm A(x_A; y_A; z_A) và B(x_B; y_B; z_B) thì:

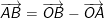
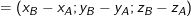
$\small \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$ $\small =(x_B-x_A;y_B-y_A;z_B-z_A)$

II. Tích vô hướng của 2 vectơ và ứng dụng của tích vô hướng

1. Biểu thức tọa độ của tích vô hướng

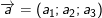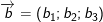• Định lý: Trong không gian Oxyz, tích vô hướng của hai vectơ $\small \overrightarrow{a}=(a_1;a_2;a_3)$ và $\small \overrightarrow{b}=(b_1;b_2;b_3)$ được xác định bởi công thức:

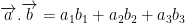
$\overrightarrow{a}. \overrightarrow{b}=a_1b_1+a_2b_2+a_3b_3$

2. Ứng dụng tích vô hướng của 2 vectơ

Tích vô hướng của 2 vectơ có có ứng dụng quan trọng, giúp ta có công thức tính độ dài của một vectơ, công thức tính khoảng cách giữa hai điểm, công thức tính góc giữa 2 vectơ, cụ thể:

i) Tính độ dài của một vectơ

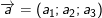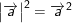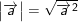
- Cho vectơ $\small \overrightarrow{a}=(a_1;a_2;a_3)$ . Ta biết rằng $\small \left | \overrightarrow{a} \right |^2=\overrightarrow{a}^2$ hay $\small \left | \overrightarrow{a} \right |=\sqrt{\overrightarrow{a}^2}$

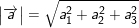
Do đó: $\small \left | \overrightarrow{a} \right |=\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}$

ii) Tính hhoảng cách giữa hai điểm

- Trong không gian Oxyz, cho 2 điểm A(x_A; y_A; z_A) và B(x_B; y_B; z_B). Khi đó khoảng cách giữa hai điểm A và B chính là độ dài vectơ 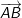$\small \overrightarrow{AB}$ . Do đó, ta có:

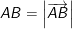
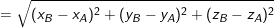
$\small AB=\left |\overrightarrow{AB} \right |$ $\small =\sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}$

iii) Góc giữa hai vectơ

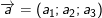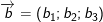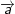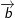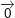- Nếu φ là góc giữa hai vectơ $\small \overrightarrow{a}=(a_1;a_2;a_3)$ và $\small \overrightarrow{b}=(b_1;b_2;b_3)$ với $\small \overrightarrow{a}$ và $\small \overrightarrow{b}$ khác $\small \overrightarrow{0}$ thì:

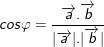$\small cos\varphi =\frac{\overrightarrow{a}.\overrightarrow{b}}{|\overrightarrow{a}|.|\overrightarrow{b}|}$ do đó:

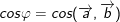
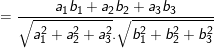
$\small cos\varphi =cos(\overrightarrow{a},\overrightarrow{b})$ $\small =\frac{a_1b_1+a_2b_2+a_3b_3}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}.\sqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}$

Từ đó, suy ra: 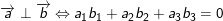$\small \overrightarrow{a}\perp \overrightarrow{b}\Leftrightarrow a_1b_1+a_2b_2+a_3b_3=0$

Hy vọng với bài viết Công thức tích vô hướng của 2 vectơ, biểu thức tọa độ và ứng dụng của tích vô hướng trong không gian ở trên của hayhochoi giúp các em giải các bài tập dạng này một cách dễ dàng. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để Hay Học Hỏi ghi nhận và hỗ trợ, chúc các em học tốt.

Công thức tích vô hướng của 2 vectơ, biểu thức tọa độ và ứng dụng của tích vô hướng trong không gian - Toán lớp 12

Tags:

Đánh giá & nhận xét